Control system analysis is intended to evaluate systems for both transient and steady state system behaviors. Transient system behavior describes the system overall performance over period of time for a given set of initial conditions and rules. For example the speed of the car (the car being the system) doesn't reach its final value the instant you press the accelerator, rather than it takes some time to reach its final value. Factors that may affect this transition of car speed could be how far you pressed the accelerator, the present condition and state of the car, the engine condition and state, road conditions, and others factors. Steady state system behavior describes the condition of the system once the transient state is exited after the transition period elapse. For example once the car (system) mentioned above reaches its final speed it is said to have reached its steady state condition, assuming that the accelerator (input) was pressed once (step function) and not followed with further changes. System steady state condition of various systems may take various times to be met. For example two different cars that have their accelerators pressed by the same amount of force may lead to two different speeds and may take different amount of time to reach their final speed. Systems can perform under two conditions:

1. Open loop system.
2. Closed loop system (feed back.)

Open loop systems are usually not as stable and reliable as closed loop systems. To stabilize system performance a feedback network is designed and implemented. Feedback is another name for closed loop system. Feedback parameters of the system can be adjusted to alter systems performance for both transient and steady state behaviors. Another name of the closed loop system is feed back control system. Systems that don't require performance stability may give up the feedback function. Some non-feedback systems of this type provide either YES-NO or ON-OFF output (bang-bang-system.) This is one type of digital systems. Having said that many digital systems require some sort of feedback network. On the other hand linear systems require feedback network for improved performance and better stability.

 

Linear systems are assumed to have an output that is linearly proportional to the input. For example the car system mentioned above has input as the accelerator and the output as the speed. While ignoring other factors affecting the car performance, the car speed would be directly proportional to the amount of force applied at its accelerator. Every equal increase of force on the accelerator results in equal amount of speed increase. If this weren't the case then the car system wouldn't be linear rather than non-linear system. Another example would be controlling the robot arm via jot stick. Every forward 1 mili meter (mm) displacement in the joystick results in 1 centi meter (cm) forward displacement in the robot arm, and every 5 mm joystick displacement would cause 5 cm forward movement of the robot arm. If a 3 mm joystick displacement causes 4 cm arm displacement then the robot arm would not be considered to be linear.

Systems behavior can be modeled by mathematical equations. These equations usually describe system steady state and transient response. One common form of system equations called time response system equations. Theoretically speaking the steady state response of a system can be found when the time parameter of these equations is set to infinity. Other parameters describing the system time response equations could be initial and external conditions that could very much interact with system performance.

Motion inducing forces, friction sources, electromechanical fabric, and other parameters along with time variable can be used to mathematically describe systems behavior.

Many systems can be analyzed for their stability without knowing their mathematical equations and thus determine what inputs and factors that lead to their instability. Once the system is found to be unstable for certain inputs the systems parameters are either manipulated to induce stability or dropped from being used. Systems can have their feedback parameters altered not only to manipulate for stability but to alter their behavior as well.

Transfer Function: Systems mathematical equations can be used to predict system behavior (or output) for any given input. An output could be the car speed, acceleration, projectile motion, voltages or currents in some electrical/electronic circuit. Input could be voltage, current, application of force, steering wheel, and so on.

For any system, the output c(t) equals to the input r(t) multiplied by the systems transfer function H(t):

 



Input Signals: Standard electrical input signals used for system simulation are impulse, step, ramp, and sinusoidal functions. Impulse function is a type of signal that has large amplitude (ideally infinity) and lasts for short period (typically 0 second). An example of impulse would be turning ON the OFF the light very fast. The mathematical representation of the impulse function d is: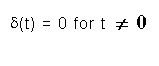





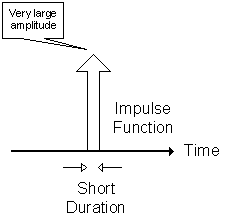
Impulse functions are used to extract the overall system behavior. It is said that the impulse input describes the systems equation or response. In other words the systems output is called the systems weighting function when the impulse function is input. That is the output of the system is similar to the systems transfer function when the system is exited with an impulse function. Also the ideal impulse function carries with it all frequencies. For example if you quickly turn on and off the light switch a close by radio tuned ON to any station (any frequency) will produce a glitch sound from the speaker. That is because the ideal impulse function (quick turn on and off of light switch) will generate a wide range of frequencies that will interfere with almost any radio station or frequency. A thunderstorm is another good example of the impulse function because you can hear its effect on almost any radio station.

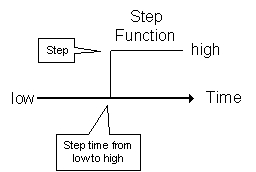
Step function is a type of signal that changes its state from OFF to ON (or ON to OFF) at certain period of time and remains there for long. An example would be turning on the light (and leave it ON for long) once you enter the room. The mathematical representation of the step function is: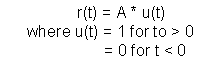





Ramp function is a type of signal that starts from 0 and increases linearly for some time then abruptly goes back to 0 and repeats again. The mathematical representation of the ramp function is: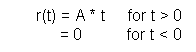





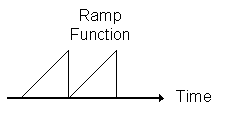
Sinusoidal input is a type of signal that changes its level (strength) periodically in a pendulum like fashion. The mathematical representation of the sinusoidal function is:

r(t) = A Sin (wt), for all times



Down * UP

Sinusoidal inputs are sometimes used to analyze the steady state of system feedback network since the sinusoidal input function carries with it large band of frequencies from 0 onwards. The sinusoidal function has advantages over the other input functions r(t) when analyzing the systems response.



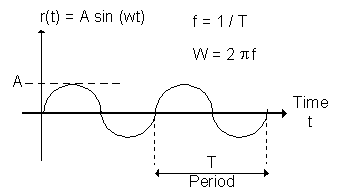
The amplitude (strength in volt or ampere) of the sinusoidal wave (sin) can be described by the following equation:

r(t) = A sin(wt)

where r(t) is the input driving force signal in volt or ampere

A is the maximum peak of the sin wave in volt or ampere

w = 2 p f (angular frequency in radian per second)

f is the frequency of the sin wave: f = 1 / T and is in cycle per second

T is the sin wave period in seconds.

Time and Frequency Domains: Time domain describes the system or signal as function of time while frequency domain describes system or signal in term of frequency. An Oscilloscope is a time domain machine (not using the Fourier analysis feature) while the Spectrum Analyzer is a frequency domain machine. System can be designed or analyzed using time analysis or frequency analysis. For sake of frequency analysis and design of systems the sinusoidal wave signal is considered. It is possible to transform system equations from time domain to frequency domain or vise versa. It is more desired to utilize the frequency domain for system design and analysis for the following reasons:

1. The design parameters in frequency domain (f) for feedback network of any system can be studied easier than in time domain.
2. Noise analysis is more convenient to analyze in frequency domain.
3. It is easier to use the frequency domain to correlate the effect of parameter changes on the overall system response.
4. The time response of the system can be obtained from its sinusoidal frequency response and vise versa.

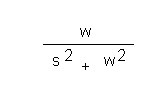
As you can see the equivalent frequency domain of the sinusoidal time domain wave Sin (wt) doesn't have the time parameter t anymore, also the s term (where s = jw) is introduced to the frequency domain equation. Recall also that w = 2 p f. The fact is that any waveform (square, triangular, ramp, and so on) can be reconstructed by summing a selected multiples of sinusoidal waves. Notice that for higher frequencies the term above becomes smaller because it is squared in the denominator. This translates into the fact that in order to reconstruct the intended waveform the frequencies belonging to higher bands carry little information about the real reconstructed waveform. Higher orders of frequencies will fine tune resolution of the intended wave shape. Assuming a perfect sinusoidal waveform, this single sinusoidal frequency is only represented by only one unique sinusoidal wave.

When the thunderstorm sparks a very large voltage is being produced for very short period of time. This is called the impulse function d(t). Remember that this spark can be heard almost on any radio station and therefore it represents an equal signal strength on all frequencies (or radio stations.) In frequency domain this impulse driving force signal becomes as follows:

Mechanical Actuation Systems: Mechanical systems translate motion or energy from one form to another in an attempt to produce a useful output. For example a mechanical may convert linear motion into rotational motion, or it may convert rotational motion to electrical energy such in electrical generators. Such a combination of electrical and mechanical assemblies is called electromechanical devices. Among the mechanical elements are cams, gears. Linkages, rack-and-pinion, chains, belt drivers, and others are among the mechanical elements that are used to produce a useful outcome. When only motion is involved (excluding forces and energy flow and analysis) then kinematics is called upon. When a robot attempts to pick an egg its arm moves in space with a controlled combination of rotational and transnational motion. Electronic signals, micro controllers, drivers, motors, solenoids, and other devices manipulate all robotic motions.

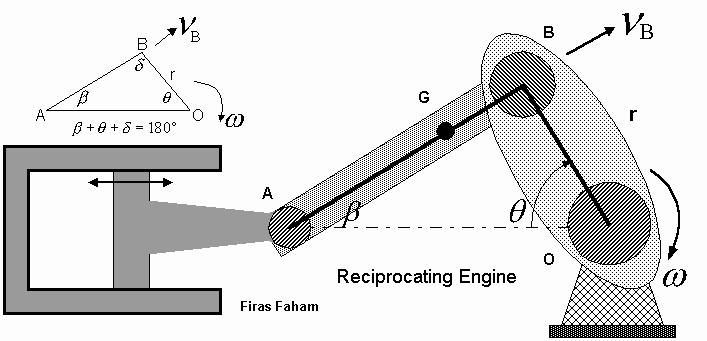
 For example if the crank OB is r = 5 in rotating clockwise, w = 1500 revolution per min, and q = 60 degrees then the velocity at point B, VB = r x w . So VB = (5/12) x (1500 x 2p /60) = 65.4 ft/sec. The VB speed is always perpendicular to the crank OB.

If AB is 14 in then the angle b can be found as follows: (5/sin b ) = (14/sin 60). This leads to b = 18 degrees. Vector velocities are perpendicular on their cranks. So crank AB velocity is perpendicular to AB. Therefore the angle between VA and VAB is 90 - 18 = 72 degrees. VA is always horizontal and points horizontally since it is not involved in a rotational motion. We already know that VA and VB are 30 degrees different since they represent point velocities and not rotational velocities.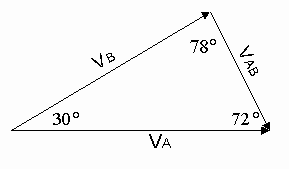

 

 

So the angle between VB and VAB is 180 - 30 - 72 = 78 degrees. According to the law of sines we then can solve for VA and VAB. (VA/sin 78) = (VB/sin 72). Given that VB is 65.4 ft/sec from above we get VA = 67.3 ft/sec. Also (VAB/sin 30) = (VB/sin 72) which leads to VAB = 34.4 ft/sec. Therefore the angular velocity of crank AB is w AB = VAB / AB = 34.4 / (14/12) = 29.5 rad/sec.

We can see from above how the rotational speed at point O of 1500 rev/min translated to a horizontal speed of 67.3 ft/sec at point A when angle q was 60 degrees and how crank AB movement relates to this Reciprocating Engine motion.